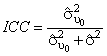
The following uses data from Menec et al. 2004. The purpose of the analysis was to examine factors associated with health care costs at the end of life, including:
Heath care costs were derived for all individuals for each of the last six months prior to death. Analyses of trends over time were conducted for 7911 individuals who had non-zero health care costs in at least four of the six months preceding death.
A cross-sectional examination of costs revealed that they were moderately to highly skewed in each time period. Therefore a logarithmic transformation was applied to produce a more normal distribution. For each individual who had a zero monthly cost, this was replaced with a positive dollar value so that the logarithm could be computed. Once the logarithmic transformation was applied to the costs the data were approximately normally distributed.
Model #1 Random Intercept and No Fixed Effects
PROC MIXED DATA=data-set-name METHOD=reml covtest;
CLASS id;
MODEL Incost = / g gcorr;
RANDOM INTERCEPT / SUBJECT=id;
TITLE2 ' RANDOM INTERCEPT ONLY';
RUN;
This model, called the null model, is typically the first model that an analyst will run when deciding whether or not to select a random effects model for the data. It contains only one parameter, which is a random intercept. It partitions the total variation in the data into within-individual and between- individual components.
The intraclass correlation (ICC) computed from this null model is a useful tool for deciding whether a random effects model might be an appropriate choice for the data. The numeric formula for the ICC is
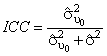
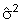 is the residual
variance.
is the residual
variance.
To illustrate:
| Cov Parm | Subject | Estimate | Standard Error | Z Value | Pr Z |
| Intercept | Id | 1.7718 | 0.03435 | 51.58 | <.0001 |
| Residual | 2.291 | 0.01629 | 140.63 | <.0001 | |
Here, 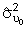 =1.77 and
=1.77 and
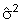 =2.29. Therefore,
ICC = 1.77/(1.77 + 2.29) = 0.44, indicating that 44% of the variation
in the data is explained by allowing the intercept to vary across
individuals. The statistically significant value for the within-individual
variation suggests the data structure is best captured by using a random
effects model
=2.29. Therefore,
ICC = 1.77/(1.77 + 2.29) = 0.44, indicating that 44% of the variation
in the data is explained by allowing the intercept to vary across
individuals. The statistically significant value for the within-individual
variation suggests the data structure is best captured by using a random
effects model
Model #2 Random Intercept and Slope
PROC MIXED DATA=data-set-name METHOD=reml covtest;
CLASS id;
MODEL Incost = time / solution g gcorr;
RANDOM INTERCEPT time / SUBJECT=id;Type=un;
TITLE2 ' RANDOM INTERCEPT and slope';
RUN;
The SAS output for the random effects variances and covariances is given below:
| Cov Parm | Subject | Estimate | Standard Error | Z Value | Pr Z |
| UN(1,1) | Id | 3.3901 | 0.07487 | 42.49 | <.0001 |
| UN(2,1) | Id | -.5742 | 0.0145 | -39.59 | <.0001 |
| UN(2,2) | Id | .1363 | 0.003553 | 38.37 | <.0001 |
| Residual | 1.4562 | 0.01158 | 125.79 | <.0001 | |
The ICC is computed using variance estimates for both the intercept and slope, as well as their covariance. For this model, ICC = (3.3901 - .5742 + .1363) / (3.3901 - .5742 + .1363 + 1.4562) = .67, indicating that 67% of the variation in the data is accounted for by allowing the intercept and the slope to vary across individuals.
An additional piece of information that can be captured from models that contain both random slopes and intercepts is the correlation between the random effects. The correlation matrix given below shows us that there is a strong negative correlation between the slope and the intercept. This means that individuals who have higher initial health care costs tend to have lower rates of change over time, and individuals who have lower initial health care costs tend to have higher rates of change over time.
| Row | Effect | Id | Col1 | Col2 |
| 1 | Intercept | 1 | 1.0000 | -0.7845 |
| 2 | Time | 1 | -0.7845 | 1.0000 |
Model #3 Random Intercept and Slope plus Additional Fixed Effects
Given that a substantial proportion of the variation in the data could be explained by inclusion of both a random intercept plus a random slope, we retained these parameters in the model. The next model also contains all of the fixed effect predictors that we were interested in testing for statistical significance. Here, age is defined as a continuous variable that was centered at the mean.
PROC MIXED DATA=data-set-name METHOD=reml covtest;
CLASS id sex cause locdth reg;
MODEL Incost = time age sex cause locdth reg / solution g gcorr;
RANDOM INTERCEPT time / SUBJECT=id TYPE=un;
TITLE2 ' FULL MODEL _ MAIN EFFECTS';
RUN;