Introduction

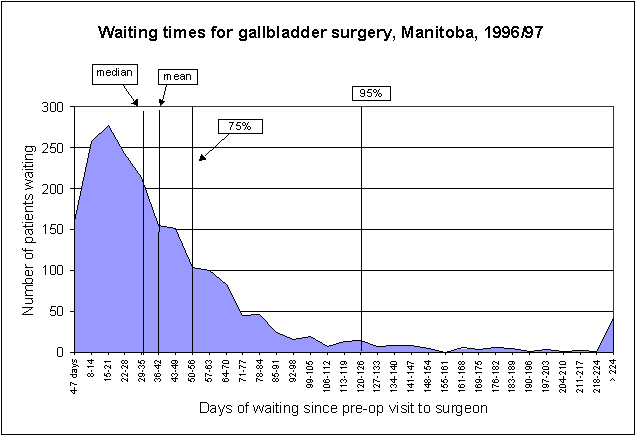
This concept discusses how to measure the confidence interval of the median, as it was done in De Coster et al.'s (2000) deliverable on waiting times which reported median waits. The wait for surgery was defined as the time between a pre-op visit to the surgeon and the date of surgery. We decided to report the median because the distribution of waits was skewed to the right, as demonstrated in the figure below, so the mean was affected by outliers.

The Issue

K.C. Carrière helped with this study, providing a formula to measure the confidence interval of the median. This statistic is used infrequently, and one that journal editors and reviewers may not be acquainted with. The method provides a confidence interval for the upper and lower bound of the rank order of the value. The bounds (number of records) must then be converted to the value they represent.

Calculating CI

A confidence interval is usually: estimate ±1.96 * S.E.

Formula provided by KC:

R = FLOOR ( ( (nobs+1) /2) - ((nobs) **0.5)/2 * 1.96);
S = CEIL ( ( (nobs+1) /2) + ((nobs) **0.5)/2 * 1.96);

Interpretation:

In this formula, KC assumed an approximation to a binomial distribution. Back to basic statistics: a binomial distribution shows the probability of x number of subjects experiencing a certain outcome when only two outcomes are possible, i.e., the probability of 0 patients surviving, the probability of 1 patient surviving, etc. etc. Probability is on the vertical axis and number of subjects is on the horizontal axis. With a large sample the binomial distribution approximates a normal distribution with mean = np, variance = npq, and standard deviation = square root of npq.

In this case, the probability in question is: the probability of waiting longer or shorter than the median. Since the median is the mid-point, then the probability (p) of waiting more than the median is 0.5 and q = 1-p = 0.5.

variance = npq = n * 0.5 * 0.5 = n * 0.25 = n/4
standard deviation = sq rt (n/4) = (sq rt n)/2
The median value is given by (n+1)/2

So: the confidence interval of the median is

[(n+1)/2] ±1.96 * (sq rt n)/2

Recall that this will only tell you the rank order of the value, so you need to go back and see which value is at the position.

Alternative Method - Bootstrapping

Since there is very little literature on using the above mathematical technique we verified the confidence measure using a highly resource intensive method called bootstrapping. This is a widely used method for statistical inference in cases where standard models are not available or are not appropriate. The method involves repeated sampling with replacement of a dataset and calculating the measure of interest on each sample. The repeated measure is then used to determine the statistic of interest.

A simple SAS macro was developed ( _boot ) for determining the mean and median of any numeric variable in a dataset and a defined confidence interval using the bootstrap method. A number of SAS macros have been developed and are available for performing jackknife and bootstrap analysis - the one generally recommend is the jackboot group of macros from SAS (see SAS Support at: http://support.sas.com/kb/24/982.html for more information). We developed our own code to better understand the technique without having to work out all of the 'bells and whistles' in the SAS developed macros.

Repeated measures using various sample datasets have shown that the method proposed by KC and the bootstrap method produce consistent results. See SAS Code listed below.