Max Rady College of Medicine
Concept: Random Effects Models - Continuous Data
Concept Description
Last Updated: 2009-08-25
Introduction
-
This concept describes random effects models for longitudinal and clustered data, focusing in particular on the statistical notation for defining these models for longitudinal data. SAS syntax for random effects models is illustrated. The concept also demonstrates the application of this SAS syntax.
This discussion will focus on methods for the analysis of continuous, normally distributed data. Continuous outcome measures used by health services researchers could include measures of health-care costs (particularly if a logarithmic transformation is applied to the data), indices of continuity of care, or measures of severity of illness.
A. Longitudinal Designs
-
Longitudinal designs are often used in population health and health services research (
Brownell M et al., 2003
and
Menec V et al., 2004
are recent MCHP examples). A good discussion of the use of administrative data for longitudinal studies is found in
Roos, Nicol, and Cageorge (1987)
.
Longitudinal data arise when repeated measurements are obtained for an individual (or unit of analysis) on one or more outcome variables at successive points in time. The analyst is interested in describing the trend over time (i.e., is it linear or curvilinear; is it increasing or decreasing), as well as whether there are significant differences in the trend across groups of subjects defined by such characteristics as income quintile, sex, region of residence, or severity of illness. One advantage of using a longitudinal design is that it is possible to separate age and cohort effects. For example, health care use may increase over time because people consume more health care resources as they get older. However, there may be differences in the rates of increase in use for individuals from different birth cohorts.
B. Clustered Designs
-
Often observations are assumed to be independent and to come from a single homogeneous population. In a multilevel design, however, observations are clustered or grouped together. Sometimes, clusters are nested within other, larger clusters. In addition to variables being observed or reported at the individual level, variables may also be observed at the cluster level. Furthermore, there is variability at the individual level, but also at higher levels. Multilevel modeling techniques allow the researcher to describe these different sources of variability and to account for them in the model.
Examples from Education:
Level 1 corresponds to individual-level data. Level 2 (and up) identify the clusters within which individuals are.
Level #: Unit of Analysis (Possible model covariates)
-
Level 1: Student (Sex, Parental Marital Status, Parental Education Attainment, or Number of Siblings)
-
Level 2: Teacher or Classroom (Classroom Size, Sex-Composition of Classroom, Teacher's Level of Education or Teacher's Years of Experience)
-
Level 3: School (Sex-Composition of School, Type - Public vs. Private)
-
Level 4: Division (Income Level of Division, Rural/Urban Status)
- Dependent Variable: Standardized test score
C. Why Use Random Effects Models
-
Random effects models are also known as multi-level models, mixed models, random coefficient models, empirical Bayes models, and random regression models. Random effects models are regression models in which the regression coefficients are allowed to vary across the subjects or between clusters. These models have two components:
-
Within-individual or within-cluster component:
an individual's change over time or cluster-specific response is described by a regression model with a population-level intercept and slope.
- Between-individual or between-cluster component: variation in individual or cluster-intercepts and slopes is captured.
D. Advantages of Random Effects Models for Longitudinal Data Analysis
-
For longitudinal studies, random effects models enable the analyst to not only describe the trend over time while taking account of the correlation that exists between successive measurements, but also to describe the variation in the baseline measurement and in the rate of change over time.
-
Subjects are not assumed to be measured on the same number of time points, and the time points do not need to be equally spaced;
- Analyses can be conducted for subjects who may miss one or more of the measurement occasions, or who may be lost to follow-up at some point during study.
There are a number of techniques for analyzing longitudinal data, including univariate and multivariate analysis of variance (ANOVA) and generalized linear models with generalized estimating equations (i.e., GEE models).
Neither univariate nor multivariate analysis of variance can be easily applied to longitudinal data that contain time-varying covariates. Both random effects models and GEE models however allow for the inclusion of time-varying and time-invariant covariates. Time-varying covariates are independent variables that co-vary with the dependent variable over time. For example, a researcher studying trends in health care utilization over time, might also want to capture data on severity of illness or degree of co-morbidity at each measurement occasion. Severity of illness/co-morbidity is likely to be an important predictor of health care utilization. It may also vary over time. Other covariates, like gender and income group either do not change over time, or are less likely to change over time.
Both random effects and GEE models allow the analyst to model the correlation structure of the data. Thus, the analyst does not need to assume that measurements taken at successive points in time are equally correlated, which is the correlation structure that underlies the ANOVA model. The analyst also does not need to assume measurements taken at successive points in time have an unstructured pattern of correlations, which is the structure that underlies the multivariate analysis of variance model. The former pattern is generally too restrictive, while the latter is too generic. With both random effects and GEE models, the analyst can fit a specific correlation structure to the data, such as an autoregressive structure, which assumes a decreasing correlation between successive measurements over time. This can result in a more efficient analysis, with improved power to detect significant changes over time.
With administrative health data, varying numbers of measurement occasions and missing observations are typically not of great concern. Very few individuals are lost to follow-up in population-based studies. Loss to follow-up will occur when individuals leave the province, or when they die. Moreover, time points of measurement will typically be equally spaced because time is often defined in terms of fiscal or calendar years, months or weeks. However, analyses of administrative data frequently include both time-varying and time-invariant covariates.
E. Statistical Model for Longitudinal Data
-
The formulae in this section can be generalized to random effects models. For multilevel data, the level 1 unit is an individual and the level 2 unit is a cluster of individuals.
The simplest regression model for longitudinal data is one in which measurements are obtained for a single dependent variable at successive time points. Let Y it represent the measurement for the i -th individual at the t -th point in time,
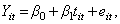
β 0 is the intercept, β 1 is the slope, that is, the change in the outcome variable for every one-unit increase in time, and e it is the error component. In this simple regression the e it s are assumed to be correlated, and to follow a normal distribution (i.e., e it ~N(0,σ)). β 0 represents the average value of the dependent variable when time=0, and β 1 represents the average change in the dependent variable for each one-unit increase in time.
The simplest random effects model is one where the intercept is allowed to vary across individuals:
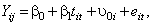
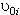 represents the influence of the individual
i
on his/her repeated observations. We can re-write this random intercept model as a two-part model, with level 1 reflecting the within-individual component:
represents the influence of the individual
i
on his/her repeated observations. We can re-write this random intercept model as a two-part model, with level 1 reflecting the within-individual component: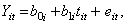
and level 2 reflecting the between-individual component:
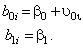
This indicates that the intercept for the i -th individual is a function of a population intercept plus a unique contribution for that individual. We assume
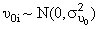 . This model also indicates that each individual's slope is equal to the population slope,
β
1
.
. This model also indicates that each individual's slope is equal to the population slope,
β
1
. When both the slope and the intercept are allowed to vary across individual the model is:
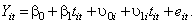
The level 1 model is the same as before:
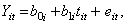
and the level 2 model is:
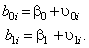
This indicates that the intercept for the i -th individual is a function of a population intercept plus some unique contribution for that individual. As well, the slope for the i -th individual is a function of the population slope plus some unique contribution for that subject. We assume
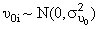 and
and 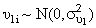 and
and 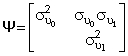 ,
,is the variance-covariance matrix of random effects. Correlation exists between the random slope and the random intercept, so that individuals who have higher values for the intercept (i.e., higher or lower values on the dependent variable at the baseline time point) will also have higher or lower values for the slope.
F. Steps in Conducting a Random Effects Analysis
-
Step 1: Exploratory Data Analysis
-
Correlations among measurements - this is useful for selecting a covariance structure for the data. The analyst might ask the following questions: Is there equal correlation between successive measurements? Does the correlation appear to decrease over time?
-
Nature of trend over time - is it linear or non-linear (i.e., curvilinear) in form? If the latter, the analyst may need to include a high-order time effect in the model, such as time
2
.
-
Heterogeneity - is variability in the measurements increasing or decreasing over time? Increasing variability suggests that the analyst will need to consider including a random slope in the model.
- Presence of outliers - are extreme observations or influential observations present on either a cross-sectional or longitudinal basis? If the data are non-normal, then the analyst may want to consider adopting a non-linear random effects model. For example, for non-normal data, the analyst might need to consider a binomial, negative binomial, Poisson, or gamma distribution to fit the data.
-
PROC GPLOT - to produce plots of the trends over time for individual subjects, or for groups of subjects defined by time-invariant covariates such as gender.
-
PROC CORR - to characterize the correlation between measurements.
- PROC UNIVARIATE - to examine means, variances, skewness, kurtosis, and to check for extreme values at each time point.
-
Fit the fixed effects
-
Select a correlation structure for the measurements
-
Fit the random effects
- Select a correlation structure for the random effects
-
which correlation structure should be fit to the data;
-
whether random intercepts and/or random slopes are necessary in the model;
- whether all of the predictor variables and one or more interaction terms should be included in the model.
Before deciding whether a random effects model is an appropriate choice for the data, the analyst should begin by conducting a thorough exploratory analysis of the data. Exploratory data analysis (EDA) techniques are used to examine:
In SAS, the procedures that may be used for EDA include:
Step 2: Fitting the Model
For continuous, normal data, SAS PROC MIXED can be used to do one or more of the following:
Step 3: Checking the Fit of the Model
The analyst will wish to determine whether the initial model that is fit to the data is an appropriate choice. Often the analyst will cycle between steps 2 and 3 to select the best model given the characteristics of the data, and the research questions of interest. Model goodness of fit statistics can be used to compare models and determine:
In addition, plots of residuals may be examined to determine the existence of influential points or extreme observations. These influential points may result in biased parameter estimates or inflated standard errors.
Step 4: Testing Hypotheses on the Data
Once the analyst has chosen a good model for the data, one or more focused hypotheses may be tested on the data. This can be accomplished via CONTRAST and ESTIMATE statements in PROC MIXED.
G. An Important Note: Coding Time in the Model
-
In a random effects model for longitudinal data, the method selected for coding the time variable will influence the interpretation of the model as well as its variance,
-
Code
t
the time variable, so that the baseline measure has a value of zero and successive measurements are incremented accordingly. Using this format, the intercept represents the mean value of the dependent variable at the baseline time.
-
Code
t
by centering the time values. For example if
t
= 6, 12, 18, 24, 30, then the centred values would be -.33, -.667, 0, .667, .33. Using this format, the intercept represents the dependent variable measurement at the midpoint of time.
- Code t so that the endpoint measure has a value of zero and preceding measurements are decremented accordingly. Using this format, the intercept represents the mean value of the dependent variable at the endpoint.
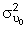 . There are three options for coding time:
. There are three options for coding time: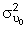 will be smaller when time is coded using method 1 than when time is coded using either of methods 2 or 3.
will be smaller when time is coded using method 1 than when time is coded using either of methods 2 or 3.The choice of which coding scheme to adopt is determined by the analyst and the researcher based on the hypotheses of interest and the interpretation of the intercept (and its variance) that is of interest to the researcher.
H. Selecting a Correlation Structure
-
Fitting the correct correlation structure to the data will ensure that estimates of the model parameters and their standard errors are unbiased. A number of different covariance structures may be selected in PROC MIXED. The most common choices are:
-
Exchangeable or compound symmetric
- assumes that correlation between all pairs of measurements are equal irrespective of the length of the time interval.
Exchangeable t 1 t 2 t 3 t 4 t 1 1 p p p t 2 . 1 p p t 3 . . 1 p t 4 . . . 1 -
Autoregressive (first order)
- with this structure, the correlations decrease over time. Observations that are one measurement occasion apart are assumed to have a correlation equal to
p
, observations two measurements apart are assumed to have a correlation equal to
p
2
, and so on. In general, observations
t
measurements apart are assumed to have a correlation equal to
p
t
.
Autoregressive t 1 t 2 t 3 t 4 t 1 1 p p 2 p 3 t 2 . 1 p p 2 t 3 . . 1 p t 4 . . . 1 -
Unstructured
- with this structure, all correlations are assumed to be different.
Unstructured t 1 t 2 t 3 t 4 t 1 1 p 1 p 2 p 3 t 2 . 1 p 4 p 5 t 3 . . 1 p 6 t 4 . . . 1
-
See the following SAS online documentation for additional examples of possible variance-covariance structures:
http://support.sas.com/onlinedoc/913/getDoc/en/statug.hlp/mixed_sect19.htm#stat_mixed_mixedecovstruct
I. Structure for Longitudinal Data
-
To use SAS for a random effects analysis of longitudinal data, the data set must be correctly structured. A longitudinal data set may have a multivariate structure or a univariate structure. In a multivariate or broad structure each individual has a single data record that contains all of the repeated measurements. In a univariate or long structure, which is required for PROC MIXED, each individual has as many data records as there are measurement occasions.
As defined previously, let Y it represent the dependent variable value for the i th individual at the t th point in time and let X it be the vector of predictor variable values for the i th individual at the t th time point. That is, X it = [X it1 X it2 … X itK ]. The ID variable is a unique identifier for each individual in the data set. The univariate data structure is:
| ID | Y it | X it1 | X it2 | … |
X
itK
|
| 1 | Y 11 | X 111 | X 112 | … |
X
11
K
|
| 1 | Y 12 | X 121 | X 122 | … | … |
| … | … | … | … | … |
… |
| 1 | Y 1 T | X 1 T 1 | X 1 T 2 | … | X 1 TK |
| 2 | Y 21 | X 121 | X 122 | … |
X
12
K
|
| … | … | … | … | … |
… |
| N | Y NT | X NT1 | X NT2 | … | X 1NTK |
In this univariate structure, each value of the dependent variable, and the associated independent variable values, is contained in a single record.
J. SAS CODE
-
This section specifies the SAS code which is used to define one or more models for longitudinal data. The required SAS syntax is given in uppercase letters, while the user specified elements are given in lower case letters.
For a model which contains only fixed effects, that is,
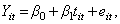
the SAS code is:
PROC MIXED DATA=data-set-name METHOD=method-of-estimation covtest;CLASS id;
RUN;
MODEL dependent-variable = time-variable / solution;
REPEATED / TYPE=correlation-structure SUBJECT=id r rcorr;
-
Examples of correlation structures:
-
Compound symmetric: TYPE=CS
-
First-Order Autoregressive: TYPE=AR(1)
- Unstructured: TYPE=UN
-
COVTEST option
- Produces asymptotic standard errors and Z-tests for each of the covariance parameter estimates
-
method of Estimation - the two most common methods are
- METHOD=REML (Restricted Maximum Likelihood - Default)
- METHOD=ML (Maximum Likelihood)
-
MODEL statement
- all fixed effects are listed after equality
-
SOLUTION option
- Requests the printing of the parameter estimates for all fixed effects in the model, together with standard errors, t statistics, and p values
-
REPEATED Statement
- Used to specify that the data for each id are from the same subject, and that the specified correlation structure should be fit to the repeated measurements. Note that the id variable must also be listed in the CLASS statement.
- R,RCORR options - produces the variance-covariance and correlation matrices for the repeated measurements
-
G, GCORR options
- Produces the variance-covariance matrix and correlation matrix for the random effects
-
RANDOM statement
- Identifies which parameters in the model are allowed to vary across subjects
- SUBJECT=id means that all records with the same value of id are assumed to be from the same subject, whereas records with different values of id are assumed to come from independent subjects. The RANDOM statement with this option produces a block-diagonal structure in G, with identical blocks.
Other notes about this syntax
For the model that contains a random intercept,
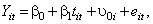
the SAS code is:
PROC MIXED DATA=data-set-name METHOD=method-of-estimation covtest;
-
CLASS id;
MODEL dependent-variable = time-variable / solution g gcorr;
RANDOM INTERCEPT / SUBJECT=id;
Notes about this syntax:
For the model that contains both a random intercept and a random slope:
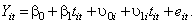
the SAS code is:
PROC MIXED DATA=data-set-name METHOD=method-of-estimation covtest;
-
CLASS id;
MODEL dependent-variable = time-variable / solution g gcorr;
RANDOM INTERCEPTtime-variable / SUBJECT=id;
See the document Numeric Example of Random Effects Models for Longitudinal Data - Continuous Data for a numeric example.
K. Reducing Computing Time for PROC MIXED
-
Computing time can be long with many clusters or subjects.
- Possible solutions:
-
Set initial values for variance-covariance estimates.
-
Use explicit nesting for hierarchical data with three or more levels (when appropriate).
- Use the DDFM=BW option.
-
Also see the SAS online documentation: MIXED --> Details --> Computational Issues --> Computing Time
http://support.sas.com/onlinedoc/913/getDoc/en/statug.hlp/mixed_sect46.htm
1. Finding and Setting Initial Values
- Take a random sub-sample using PROC SURVEYSELECT. There are various methods of selecting a random sample (stratified-sampling, cluster-sampling, simple random sampling, etc.), but for the purpose of setting initial values, the type may not be important.
- See the SAS online documentation for further details of the various methods.
http://support.sas.com/onlinedoc/913/getDoc/en/statug.hlp/surveyselect_sect7.htm
- Example of SAS code for simple random sampling (SRS) without replacement:
PROC SURVEYSELECT DATA=indata OUT=outdata
NOPRINT METHOD=SRS RATE=## SEED=##;
RUN;
- Run PROC MIXED using the random sample and look at the variance-covariance output.
- Run PROC MIXED using the full dataset with the PARMS line SAS code to set initial values.
- There are two methods: (i) manually enter the variance-covariance estimates, or (ii) identify the variance-covariance output SAS dataset from the random sub-sample PROC MIXED output.
(i) PARMS (#) (#) (#);
(ii) PARMS / PARMSDATA=var_cov;2. Using Explicit Nesting
- For data with multiple clustering structures, sometimes clusters are nested within another cluster.
- Nested Example: Students --> Class --> School
- Non-Nested Example:
- Clustering 1 - Students in the same class
- Clustering 2 - Kids in the same neighborhood
- SAS code for explicit nesting where l2_cluster denotes 2nd level clustering and l3_cluster denotes 3rd level clustering:
RANDOM INT / SUBJECT = l3_cluster;
RANDOM INT / SUBJECT = l2_cluster (l3_cluster);3. Using the DDFM=BW option
- This makes SAS use a different method to compute the denominator degrees of freedom for fixed effects.
- Fixed effects parameter estimates and variance-covariance estimates (along with their standard errors) are virtually the same.
- Degrees of freedom are much higher, however.
- See the SAS online documentation for further details: MIXED --> Syntax --> MODEL --> DDFM=
http://support.sas.com/onlinedoc/913/getDoc/en/statug.hlp/mixed_sect15.htm#stat_mixed_mixedddfm
- SAS code:
MODEL outcome = ... / DDFM=BW;4. SAS Code for all suggestions together (Random Intercept Model):
PROC MIXED DATA=indata;
CLASS l2_cluster l3_cluster;QUIT;
MODEL outcome = v1 v2 v3 / DDFM=BW;
RANDOM INT / SUBJECT = l3_cluster;
RANDOM INT / SUBJECT = l2_cluster(l3_cluster);
PARMS (##) (##) (##);
Related concepts
Related terms
References
- Brownell M, Lix L, Ekuma O, Derksen S, Dehaney S, Bond R, Fransoo R, MacWilliam L, Bodnarchuk J. Why is the Health Status of Some Manitobans Not Improving? The Widening Gap in the Health Status of Manitobans. Winnipeg, MB: Manitoba Centre for Health Policy, 2003. [Report] [Summary] (View)
- Diggle PJ, Liang KY, Zeger SL. The Analysis of Longitudinal Data. Oxford, United Kingdom: Univeristy Press; 1994.(View)
- Menec V, Lix L, Steinbach C, Ekuma O, Sirski M, Dahl M, Soodeen R. Patterns of Health Care Use and Cost at the End of Life. Winnipeg, MB: Manitoba Centre for Health Policy, 2004. [Report] [Summary] (View)
- Omar RZ, Wright EM, Turner RM, Thompson SG. Analysing repeated measurements data: a practical comparison of methods. Statistics in Medicine 1999;18(13):1587-1603. [Abstract] (View)
- Roos LL, Nicol JP, Cageorge SM. Using administrative data for longitudinal research: comparisons with primary data collection. J Chronic Dis 1987;40(1):41-49. [Abstract] (View)
- Singer JD, Willett JB. Applied Longitudinal Data Analysis: Modeling Change and Event Occurance. New York, NY: Oxford University Press; 2003.(View)
- Singer JD. Using SAS PROC MIXED to fit multilevel models, hierarchical models, and individual growth models. Journal of Educational and Behavorial Statistics 1998;24(4):323-355.(View)
- Twisk JWR. Applied Longitudinal Data Analysis for Epidemiology: A Practical Guide. Cambridge, UK: Cambridge University Press; 2003.(View)
- Verbeke G, Molenberghs G. Linear Mixed Models for Longitudinal Data. New York, NY: Springer-Verlag; 2000.(View)
- Wu YW, Clopper RR, Woolridge PJ. A comparison of traditional approaches to hierarchical linear modeling when analyzing longitudinal data. Research in Nursing and Health 1999;22(5):421-432. [Abstract] (View)
Keywords
- statistics
Request information in an accessible format
If you require access to our resources in a different format, please contact us:
- by phone at 204-789-3819
- by email at info@cpe.umanitoba.ca
We strive to provide accommodations upon request in a reasonable timeframe.
Contact us
Manitoba Centre for Health Policy
Rady Faculty of Health Sciences,
Room 408-727 McDermot Ave.
University of Manitoba
Winnipeg, MB R3E 3P5 Canada
